Symmetric Cryptography

Symmetric ciphers use the same key for encryption and decryption. Plaintext gets encrypted with a key into ciphertext and then decrypted back into plaintext using the same key.

One-Time Pad

One of the simplest examples of a symmetric cipher is the “One-Time Pad” (OTP).

To encrypt, we simply take the plaintext message (p) and XOR it with a key (k) of the exact same length. The resulting ciphertext (c) is of the same length as p and k.

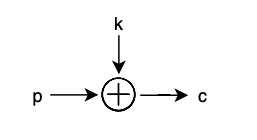
p ^ k = c

Decrypting the ciphertext back into the plaintext message is just as easy thanks to the associative and commutative properties of the XOR operator. Simply XOR the ciphertext with the key to obtain the plaintext message.

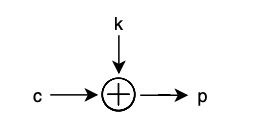
c ^ k = p

Upsides

OTP is actually a very powerful encryption technique. In fact, it’s so powerful that it’s said to have “perfect secrecy”. In other words, without the key, it’s impossible to decrypt the ciphertext back into a plaintext message. When we say impossible, we really mean impossible. No future supercomputer will ever be able to crack OTP. How are we so sure? Because there is no statistical relationship between the ciphertext and the plaintext message. None.

Sounds pretty powerful right? So why even continue reading? Haven’t we already found the best encryption technique out there? Well, not exactly. There’s more to the story.

Downsides

Suppose you want to encrypt a 2GB file on your computer and upload it to the cloud, with OTP that means you’re going to need a 2GB key. That’s not a very efficient use of space. Speaking of keys, how are we going to store or transport the key without anybody else seeing it? As we go on, you’re going to see that a good encryption technique is not just about secrecy, but also about practicality.

Another issue with OTP is that we can never reuse the same key. Say we encrypt two different messages p1 and p2 with the same key:

p1 ^ k = c1
p2 ^ k = c2

What happens if we XOR c1 and c2?

c1 ^ c2 = p1 ^ p2

The XOR of c1 and c2 yields the XOR of plaintexts p1 and p2. Why is this noteworthy? Let’s denote the result of p1 ^ p2 as s. If we already know that the plaintexts p1 and p2 contain, say, English words, we can guess an English word that has a good chance of showing up in either plaintext message and then slide this word along the length of s, XORing it at each position.

If the result of these XORs at any position looks like it might be another English word, we’ve likely uncovered a segment of both of the plaintext messages.

s = p1 ^ p2
if s ^ [guess] == [English word]; then
    guess = part of p1 (or p2)
    English word = part of p2 (or p1)
fi

For example, let’s guess that the word “the” occurs in one of the plaintext messages. We position “the” at the beginning of the string s and XOR them together, if the result looks like it could be all or part of another English word, then we have likely uncovered the first two substrings of both plaintext messages (i.e. “the” and whatever other word we uncovered).

We continue sliding the word “the” along the entire string, s, until we’ve uncovered all instances of it in either p1 or p2.

We can then try different words and sliding those along s until we’ve uncovered more words. In general the more words we uncover the easier it becomes to guess the next word in a phrase.

We can continue this trial-and-error attack known as crib dragging until we’ve uncovered the entirety of both plaintext messages - no key required!

Not to worry, there are more practical encryption techniques out there.

Broadly speaking, symmetric cryptography splits into two types, Stream Ciphers and Block Ciphers.

---

Stream Ciphers

In order to solve the problem of having to store and transport a very large key, we can instead use something like a Keystream Generator. A Keystream Generator takes a relatively small fixed length key and uses it to generate an infinitely long psuedo-random sequence of bits for our keystream. A nonce (number used once) seeds the key and ensures our keystream is different every time, even if we re-use the same key. In practice, the nonce is usually just a counter and it doesn’t need to be kept a secret.

Upsides

One of the benefits of this technique over OTP is that we can now generate whatever length keystream we need to match the length of our plaintext message. No more 2GB key to match our 2GB file because we’re generating a keystream on the fly.

Another upside is that stream ciphers generally run faster on hardware than block ciphers like AES, we’ll talk more about that later.

Downsides

One of the downsides with stream ciphers is that tampering with the ciphertext is not very obvious. Suppose we flip a few bits of ciphertext, that ciphertext will then XOR with the keystream and potentially flip some of the bits of the plaintext.

Not a big deal, right? Well that depends. If the modification is very subtle then it may not be very obvious that the ciphertext has been tampered with. What if the account number is changed in a banking transaction? What if the GPS coordinates are off by a few degrees? With block ciphers, any tampering with the ciphertext is likely to be obvious because the plaintext probably won’t make any sense…

This isn’t a deal breaker with stream ciphers though, because there are ways to protect the integrity of a message, but it’s something to keep in mind.

Another thing to be careful of with stream ciphers is that the keystream must truly be statistically random otherwise an attacker will be able to guess the sequence of bits. Statistically random means that if we were to generate a couple billion 0’s and 1’s, there would be no way to guess whether the next bit is a 0 or 1 with any better than 50% accuracy.

---

Block Ciphers

Block ciphers are a more popular type of symmetric cipher. They work by taking an input of fixed size and returning an output of the same size (usually 128 bits).

The most popular type of block cipher is called an SP-Network; SP stands for Substitution Permutation. The name SP-Network refers to the fact that we apply a logical network of substitution and permutation operations on a single block (fixed size) of bytes to obtain a specific algorithm. In other words, bytes of an input block are repeatedly replaced and swapped over a series of rounds until we form a block of ciphertext.

All modern block ciphers are SP-Networks, but keep in mind that others do exist (e.g. Feistel Ciphers).

AES

The most popular type of SP-Network is the Advanced Encryption Standard (AES). It was ratified in 2001 after two Belgian cryptographers, Vincent Rijment and Joan Daemen, won a competition to find the best encryption algorithm.

AES is by far the strongest, most tested, easiest to understand (and implement) block cipher that we have today. It’s also one of the fastest to run on a lot of hardware.

In AES, each block is always 128 bits (16 bytes) in size while key size can be 128, 192, or 256 bits.

The way we use a block cipher is called a mode of operation, and so when we talk about block ciphers, we always combine it with a mode of operation.

We’re going to talk about four different modes of operation for AES: ECB, CBC, CTR, and XTS. We’ll also talk about a variant of CTR mode called GCM.

ECB

ECB stands for Electronic Code Book. The name stems from back when spies used physical codebooks to encrypt and decrypt messages.

The concept of ECB is simple to understand. We take plaintext message block 1 (first 128 bits), M1, and we encrypt it with our key and algorithm, Ek, to get ciphertext 1, C1. We then take plaintext message 2 (next 128 bits) and we encrypt it with our key and algorithm to get ciphertext 2, we repeat this process until we reach the end of our plaintext message.

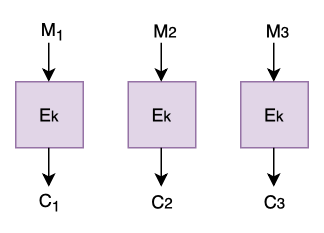
If our message is not an exact multiple of 128 bits (usually the case!), we pad it using a padding scheme.

So we’ve encrypted our message, and as an added bonus, we can encrypt each message block in parallel because no two blocks are co-dependent. Sounds great right? Not so fast!

What happens if two message blocks are the same? There is a very famous image that illustrates this problem beautifully called the “ECB Penguin” and it looks like this:

In the first image we have the original Linux logo, and in the second image we have the same logo with its pixels encrypted using ECB mode.

Notice that even though the colours are obfuscated, we still have way too much information about the original image. This is because when two message blocks are the same and they get encrypted with the same key and algorithm, the result will be the same block of ciphertext.

Knowing that two message blocks are the same is very useful information that you do not want divulged in a secure system. Because of this problem, ECB mode is considered weak and is not recommended for use. So what other options are out there?

CBC

CBC stands for Cipher Block Chaining. In this mode of operation, we take the output of one block and pass it into the input of the next block using XOR. The input of the first block is XOR’d with a random block of data called an Initialization Vector (IV) (not to be confused with a nonce!).

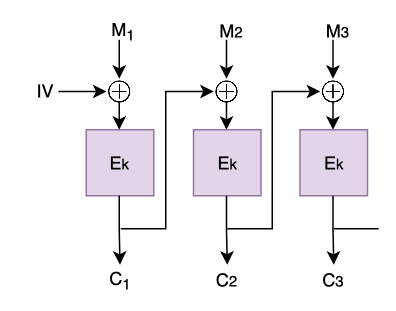
Because each message block gets XOR’d with a different input before it gets encrypted, we’re no longer concerned about identical message blocks encrypting into identical ciphertext blocks. So the problem we had with ECB is solved.

However, it came at a price! Notice that we now have to wait for the previous block to finish encrypting before we can move on to the next block; so we can expect this mode of operation to be a bit slower.

So, good but not great. Fortunately there’s a better way.

CTR

CTR is an abbreviation for Counter Mode. This mode of operation is going to blow your mind a little but it’s surprisingly straight forward.

Essentially, we’re going to take a counter and encrypt that instead of our message block. We’re then going to XOR the result of that encryption with our message block to produce our ciphertext.

So in other words, we’re going to use our block cipher as a stream cipher because our encrypted counter acts like a keystream generator. As a result, we’ll be able to parallelize our operation again without sacrificing security.

Don’t worry if you’re having trouble conceptualizing this. Here’s a diagram that does a better job than words:

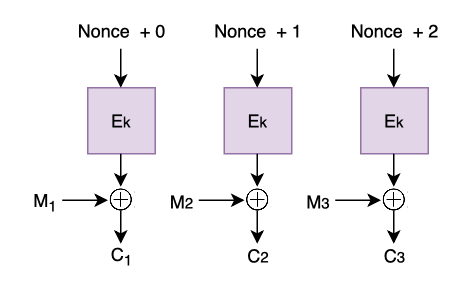
The nonce should always start from a unique value for a specific set of messages. We then increment this value for each message block to ensure it lives up its name and is never repeated.

Notice that like CBC mode, C1 and C2 are unlikely to ever be the same when M1 is identical to M2.

Counter mode is the most modern mode of operation of AES. The final mode we will talk about for AES is just a variant of CTR mode called GCM mode.

XTS

XTS stands for XEX-based Tweaked codebook mode with ciphertext Stealing. That’s a lot of words for a 3-character acronym, but don’t be intimidated!

Let’s start with XEX:

XEX stands for XOR Encrypt XOR and refers to a general mode of operation where the plaintext message block is XOR’d with a 128-bit value called a “tweak”, encrypted, and then XOR’d again with the tweak¹.

“Ciphertext stealing” refers to a technique that enables encrypting partial message blocks by “stealing” ciphertext from the last full block. The following diagram illustrates ciphertext stealing.

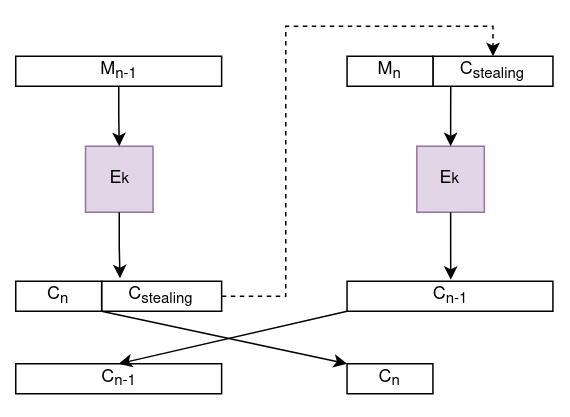
Notice that a segment of ciphertext produced from the last full plaintext message block, Cstealing, is appended to the partial plaintext message block, Mn, to generate one full block. As a result, padding the partial message block is not necessary.

Ciphertext stealing is not exclusive to XTS mode, and is especially desireable in applications where padding can be expensive, like in storage devices. As a matter of fact, XTS-AES was designed specifically for encrypting sector-based storage devices (as you’ll see next)².

Now that we’re caught up on the terminology, let’s say we’re encrypting data in sector-based storage. XTS works by using the sector-number of the sector in which the data resides as the plaintext tweak value, i, encrypting it with a key, k2, to produce the encrypted tweak value, T, and XORing T with M. The result of that operation is then encrypted using a separate key, k1, and XOR’d again with T to produce C.

The diagram below illustrates the way XTS-AES works more clearly.

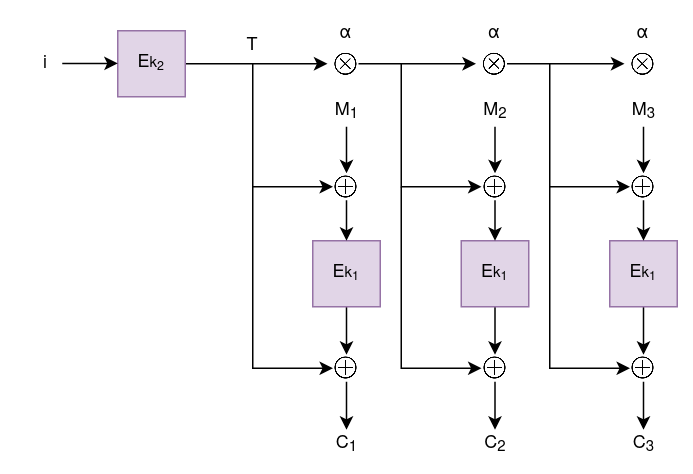
Notice also that subsequent message blocks require the encrypted tweak, T, to be multiplied by a factor, α³. This prevents subsequent identical message blocks from encrypting into identical ciphertext blocks.

In the context of sector-based storage, XTS has a number of advantages over CBC and CTR modes of operation, namely:

1. CBC mode requires operations on individual blocks be performed in series (i.e. one block at a time), whereas XTS operations on individual blocks can be parallelized (i.e. all blocks simultaneously).

2. CBC mode is vulnerable to cut-and-paste attacks, wherein copying a sector of ciphertext from one position to another will decrypt into the same plaintext in the new position, except [perhaps] the first block of that sector. As a result, an attacker who is allowed to decrypt one sector but not another, can manipulate the ciphertext of the disallowed sector in order to produce a known plaintext.

3. CTR mode, without the use of authentication tags, allows an attacker to flip bits of ciphertext and still likely have the decrypted plaintext make sense. In other words, tampering with the message is likely to go undetected.

GCM

GCM stands for Galois Counter Mode. GCM mode is similar to CTR mode but includes a Message Authentication Code (MAC) called a Galois Message Authentication Code (GMAC).

Recall that CTR mode works similarly to a stream cipher and that an issue with stream ciphers was that tampering with the ciphertext can go undetected. With GCM mode, a GMAC is computed over the ciphertext and any associated unencrypted data to ensure that not only is our message secure but it is also untampered with.

AEAD

AES-GCM is an example of Authenticated Encryption with Associated Data (AEAD).

In the real world, all of our ciphers require a way to authenticate the ciphertext and any associated data. For example, if we are using a VPN, we normally use IPsec to both encrypt and authenticate our message, but we also use it to authenticate the unencrypted header of the IP packet.

We already know that AES-GCM is an AEAD for block ciphers, but what about stream ciphers? With stream ciphers we normally protect the integrity of our message by computing a MAC or Hash-Keyed MAC (HMAC). So if we know that we’re going to need a MAC, why not build that into the standard? That’s where ChaCha20_Poly1305 comes in.

ChaCha20 is arguably the best stream cipher out there right now and the only one that sees some serious use today (Android). Poly1305 is a MAC that normally goes with it. The two have been combined to form the AEAD known as ChaCha20_Poly1305 which is currently the most popular AEAD for stream ciphers.

ChaCha20_Poly1305 is probably just as strong as AES-GCM and choosing between the two largely depends on the hardware it will be running on. AES-GCM runs faster on processors with AES-dedicated hardware acceleration (i.e. AES_NI), while ChaCha20_Poly1305 runs faster on processors without dedicated AES hardware acceleration.

In summary, it is recommended to use an AEAD mode of operation as they provide a means of encrypting and authenticating payloads and associated data by default.

1. The term “tweak” refers to a third input (aside from the plaintext message and the key) that is used for generating ciphertext. You can think of it as serving a similar purpose to an IV or a nonce. ↩

2. Sector-based storage refers to a hardware abstraction for data storage in which data is managed in fixed-sized units of data called “sectors”. ↩

3. α corresponds to decimal 2, and represents a primitive element of GF(2^128) where GF stands for Galois Field (see Menezes et. al, Handbook of Applied Cryptography, CRC Press, 1997). ↩